Experimentovanie čitateľov – diel tretí

Samuelsonova učebnica Economics obsahuje široké spektrum návodov, príkladov, matematických vzorcov, tabuliek a inštruktívnych grafov vhodných na premýšľanie o hospodárstve a tvorbe vlastných predstáv o ňom. Za určitý nedostatok možno považovať to, že sa málo zdôrazňuje hypotetickosť uvádzaných situácií a to, že väčšina použitých modelov patrí do sféry mechaniky a nie živých sociálnych organizmov.

Čitateľ si tieto súvislosti môže overiť štúdiom príkladov v už skôr spomínanej 24. kapitole. V dôsledku týchto chýbajúcich upozornení ľahkovernejší čitatelia môžu podľahnúť ilúzii, že tak, ako je to v oných modeloch nevyhnutne, musí byť aj v hospodárskej realite, čo je však zrejmý sebaklam. Nechceli by sme však vyvolať o tom zlý dojem a podsunúť Samuelsonovi zámer, že to robil uvedomele a už vôbec nie cieľavedome, on sa len, zrejme, úporne snažil vyjsť v ústrety čitateľom tak, aby boli veci jednoduchšie a zrozumiteľnejšie. Čo mu možno azda predsa len vytknúť je aj to, že neupozorňoval na to, že toto je náš abstraktný model alebo jednotlivý a jedinečný príklad vzatý z dnes už minulej reality a úplne iná môže byť terajšia a budúca živá hospodárska realita.

 

Nehovoriac o tom, že celok je ešte komplexnejší ako jednotlivé prípady, ktoré rieši. Na druhej strane, ako sme už ukázali skôr aj relatívne jednoduché matematické modely snažiace sa opísať ekonomické, väčšinou izolované prípady a situácie môžu pri hlbšej analýze ukázať vyvíjajúce sa veľmi komplexné správanie. Taká analýza si však vyžaduje solídne matematické vedomosti a analytické zručnosti a najmä vysokú abstraktnú predstavivosť, čo pre bežného čitateľa nie je samozrejmá danosť. Našťastie, ako sme už takisto skôr naznačili, svitá aj pre takých čitateľov nádej na lepšie pochopenie podobných modelov vďaka IKT, Internetu a produktom a službám komputačnej inteligencie. Už len použitie modelov a experimentovanie s nimi v Excele znamená v tomto smere výrazný pokrok, o čom sa čitateľ mohol presvedčiť už v prvom a druhom našom príspevku. V tomto (treťom) príspevku sa budeme snažiť pomôcť vopred nepripravenému čitateľovi experimentovať s modelom duopolu pomocou softvérového prostredia iDMC (interactive Dynamical Model Calculator). Za tým účelom však musíme model duopolu uviesť v matematickej forme.

Predpokladajme, že výrobca A dodáva na trh množstvo tovaru x a výrobca B úplne rovnaký tovar ale v množstve y. Obaja výrobcovia sa líšia v úrovni hodnôt svojich marginálnych nákladov m a n, pričom ich podiel m/n = k, čo je vhodné v záujme zjednodušenia analýzy. Oneskorenie reakcie výrobcov sme označili symbolmi a resp. b. Nebudeme čitateľa zaťažovať matematickým odvodzovaním modelu a tak priamo píšeme, že

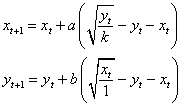
Aby sme mohli uvedenú dvojrozmernú sústavu použiť na experimentovanie v iDMC, musíme ju upraviť do podoby, ktorú iDMC požaduje, takže

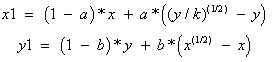
Program prijme aj verziu

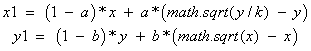
Čitateľ nájde návod na využívanie programu iDMC priamo od konštruktérov programu M. Lines a  A. Medio na stránke: iDMC/COMPILING at master· antoniofabio/iDMC · GitHub.

Čitateľ ktorý dobre ovláda angličtinu a má hlbší záujem o problematiku experimentovania s ekonomickými modelmi, si môže pozrieť esej L. Andrášika uverejnenú vo vydavateľstve De Gruyter: „COMPUTATIONAL QUALITATIVE ECONOMICS – USING COMPUTATIONAL INTELLIGENCE FOR ANDVANCED LEARNING OF ECONOMICS IN KNOWLEDGE SOCIETY“. Je na tejto internetovej adrese.

Vyššie uvedený vzorec sme vložili do programu, v ktorom to vyzerá tak, ako je to nasnímané na obr. 1. Čitateľ, ktorý má vážny záujem naučiť sa experimentovať v programe iDMC, poskytneme všestrannú pomoc. Ak si však čitatelia netrúfajú na iDMC, môžu si situáciu experimentovať v Excele, aj keď to nie je natoľko inštruktívne a priamo pozorovateľné v pohybe ako v iDMC. Ako vidno, na snímke experimentovať možno s tromi parametrami, teda všetkými, ktoré obsahuje model a navyše sa môže experimentovať aj so začiatočnými objemami výrobcov posielanými na trh. Opis progranu iDMC nájdete na nasledovnej adresehttps://code.google.com/archive/p/idmc/. A tu sú základné otázky spojené s programom. 

Prvé tri simulácie sme uskutočnili s ad hoc vybranými parametra a = b a k , ktoré sme v každom jednotlivom prípade ponechali nemenné. Menili sme však vo všetkých troch prípadoch začiatočný podiel objemu tovarov oboch výrobcov posielaných na trh. Získané obrázky z troch experimentov sme premietli priehľadne na seba a tak sme získali obr. 2. Uvedeným postupom sa nám podarilo dokázať a zreteľne ukázať kvalitatívnu nerovnorodosť celého kvadrantu x ´ y, t. j. že existujú tri kvalitatívne od seba sa líšiace oblasti oddelené od seba uzavretými invariantnými krivkami, UIK_atrakt a UIK_repel. Oblasť vnútri UIK_repel je bazénom atrakcie Cournotovho rovnovážneho bodu E. Oblasť medzi oboma UIK je bazénom atrakcie UIK_atrakt,

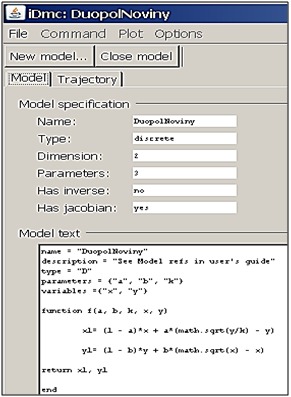
Obrázok 1 Snímka z iDMC s modelom duopolu

a oblasť za touto krivkou je nehomogénna, ale jej deväť parciálnych častí je jej bazénom atrakcie, avšak nehomogenitu tejto oblasti nebudeme rozoberať, lebo je to matematicky veľmi náročné a relevantný ekonomický význam má len bazén atrakcie bodu E, tmavšia zelená farba na obr. 2.

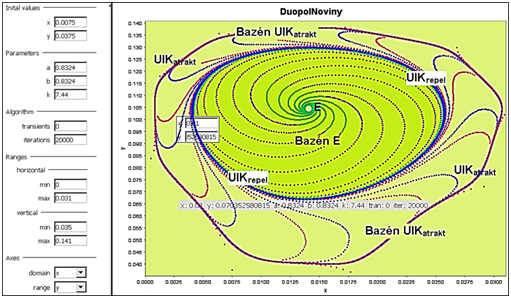
Obrázok 2 Výsledok prvých troch experimentov v iDMC

V nasledujúcom prípade experimentujeme hodnotou parametra k, pričom sprvu začiatočný pomer tovarov producentov A, resp. B ponechávame nemenný. Na obr. 3 ukazujeme výsledok experimentu, keď sme zmenšovali dva krát hodnotu k = 7.43775 o hodnotu Dk = 0.01. Z toho

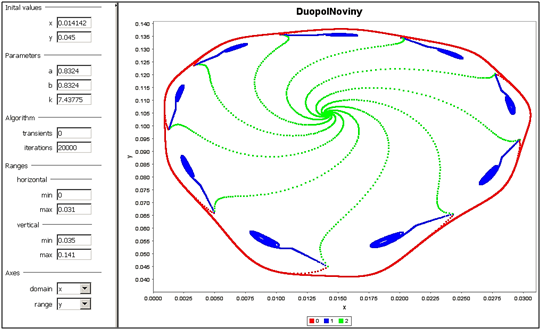
Obrázok 3 Experimentovanie s hodnotou parametra k

ľahko prídeme k záver, že pri hodnote k = 7.42775 vznikne kvalitatívne úplne nová situácia s deviatimi atraktívnymi fókusy a na modrých trajektóriách vidíme aj deväť zlomov z čoho môžeme usudzovať na existenciu deviatich sediel, čo v nasledujúcom experimente skúsime overiť. Na obr. 3 ukazujeme výsledok ďalšieho experimentu, ktorý sme získali tak, že sme Obrázok 3 Zviditeľnenie deviatich sediel

k začiatočnej súradnici y pridali pri druhom behu hodnotu Dy = 0.0000006, takže keď predtým trajektórie pri deviatich sedlách odbočili doľava a smerovali do fókusov, po tejto drobnučkej zmene odbočili trajektórie doprava a smerujú do rovnovážneho bodu E. Treba upozorniť, že iba čírym prezeraním snímok z uskutočnených experimentov môže vzniknúť falošná predstava, že sa stavový bod, t. j. pomer množstiev x voči y homogénneho tovaru umiestňovaného na trh pohybuje v smere naznačených čiar. V komputačnej realite však stavový bod poskakuje medzi naznačenými čiarami, čo sme zviditeľnili na obr. 4. Ako vidno

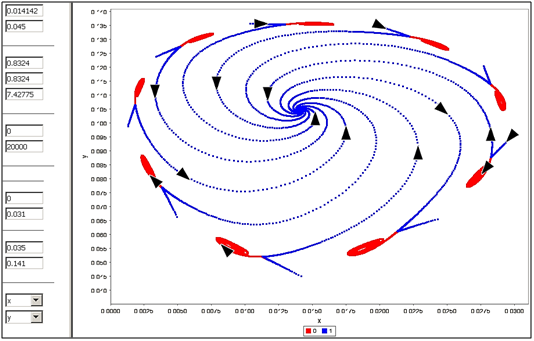
Obrázok 4 Preskakovania stavového bodu zo špirály na ďalšiu s vynechaním jednej

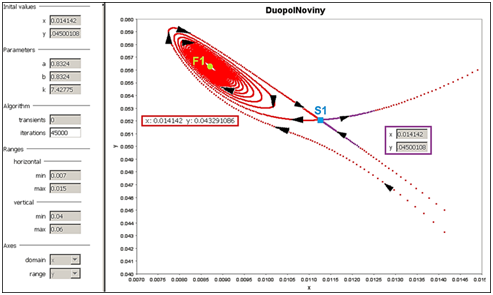
na snímke z ďalšieho experimentu, stavový bod preskakuje v pomerne veľkých skokoch z jednej špirály na ďalšiu pričom vždy jednu vynechá a veľmi pomaly sa približuje k bodu E. Z toho možno usúdiť, že tieto výrazné zmeny štruktúry dodávok budú klásť enormné nároky na to, aby obaja výrobcovia dokázali v rozumnom čase prispôsobiť k tejto potrebe svoje výrobné kapacity. Na ďalší experiment sme vybrali okolie bodov S1 a F1 aby sme podrobnejšie ilustrovali smerovanie vetiev sedlového bodu S1, obr. 5.

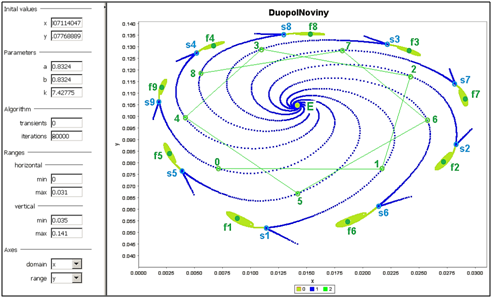
Obrázok 5 Detail okolia bodov S1 a F1

Obrázok 6 Fixné body v rutine iDMC Cycles

Doteraz sme experimentovali s využitím rutiny iDMC nazvanej Trajectory. Na zviditeľnenie a pomerne presné odhadnutie hodnôt fixných bodov S, F a E sa výborne hodí rutina iDMC s názvom Cycles. Na obr. 6 vidíme výsledok experimentu pomocou tejto rutiny. Zelené bodky znázorňujú fixné atraktívne body, teda Bod E a body F a modré zase sedlá S.

Predviedli sme ukážky a konkrétne zdroje i návody ako možno experimentovať v prostredí iDMC. Z experimentov, ktoré sme urobili si môže čitateľ urobiť aspoň predbežnú predstavu o tom, že viaceré modely uvádzané Samuelsonom majú mechanický charakter, teda ontologicky vzaté predstava o hospodárstve je taká, že má vlastnosti mechanického systému. V skutočnosti je však hospodárstvo veľmi komplexný sociálny organizmus v ktorom sú jeho tvorcovia, teda ľudia v mnohorakých funkciách prepojení medzi sebou do ešte komplexnejších horizontálnych a vertikálnych sietí. Preto robiť závery zo Samuelsonovej učebnice o objektívnej hospodárskej realite treba veľmi opatrne a nenechať sa skĺznuť do viery, že sa v nej pojednáva priamo o nej, pretože v množstve prípadov sa riešia subjektívne vytvorené mechanické systémy alebo sa berú údaje z minulej reality, ktoré však nová realita nemusí (závisle a otrocky) nasledovať.

Pokračovanie o týždeň!