Komplikácie na strane ponuky izolovaného trhu
Pred týždňom sme sa pokúsili priblížiť neoklasické predstavy o fungovaní izolovaného trhu niekoľkými vstupnými predpokladmi, ktoré sa však môžu dostať aj do polohy predsudkov a použili sme aj tri grafy z Excelu. Vo výklade sme neuviedli jeden z hlavných predpokladov, ktorý sa ľahko premení na predsudok: …”vývoj na trhu má tendenciu vždy smerovať k rovnováhe“. Sú však aj ďalšie neoklasické predpoklady, ktoré sa v myšlienkovom skrate ľahko môžu premeniť na predsudky, fixné idey a decepcie pri prenose na objektívnu hospodársku realitu.
V dnešnom príspevku sa zameriame na niektoré z nich na strane ponuky izolovaného trhu. Na tento účel sa pre prvotné porozumenie komplikácií ktoré vznikajú na strane ponuky už vo veľmi jednoduchých podmienkach výborne hodí teória konkurencie A. A. Cournota, ktorá sa preslávila najmä ako Cournotova teória duopolu.
Pripomeňme si, že A. A. Cournot predbehol P. A. Samuelsona skúmaním izolovaného trhu zhruba o viac ako sto rokov (Cournot vydal svoju knihu v roku 1838), Samuelson sa však na neho priamo neodvoláva a duopolom sa nezaoberá. Jeho učebnica sa venuje konkurencii až v 25. kapitole. Z hľadiska prvotného porozumenia neoklasických predpokladov o správaní izolovaného trhu je však teória duopolu ako sme už naznačili skôr dôležitá.
Hneď na začiatok je potrebné si všimnúť kľúčové predpoklady Cournotovho modelu izolovaného trhu. V prvom rade nezvažuje komplikácie na strane dopytu a jednoducho predpokladá, že dopyt sa prispôsobuje ponuke proporcionálne – predpokladá sa teda že dopyt má vlastnosti izoelasticity (dokonalá hyperbola, viď graf obr. 1), t. j., že zmena ceny je recipročná k zmene množstva ponúkaného tovaru.
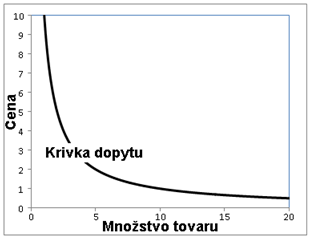
Obrázok 1 Izoelastická krivka dopytu
Prirodzene to je pochopiteľný ústupok na zjednodušenie výkladu, ale na škodu správneho porozumenia nie je dostatočne jasne zdôraznené, že je to iba subjektívna predstava a v realite to presne tak nemusí byť a spravidla ani nie je.
Ďalšie predpoklady použité pri konštrukcii modelu duopolu sú:
- Ponuku tvoria dvaja producenti s rozdielnymi marginálnymi (hraničnými) nákladmi;
- Vyrábaný tovar je úplne rovnaký čo do kvality, dodávka na trh sa líši v množstvách;
- Producenti si navzájom konkurujú množstvami dodávaného tovaru;
- Producenti majú za cieľ maximalizovať svoj zisk;
- Reakcie producentov sú okamžité len čo sa im objaví a ozrejmí situácia z predchádzajúceho kroku;
- Evolúcia na trhu má charakter krokového (iteračného) procesu;
- Proces v ľavej a spodnej časti súradnicovej sústavy má tendenciu viesť k rovnováhe, pretože reakčné krivky sú naklonené k sebe ako to vidno na obr. 2 . Na obr. 3 zviditeľňujeme iteračný proces vedúci k rovnováhe množstiev dodávaného tovaru na trh v štruktúre 1:2.
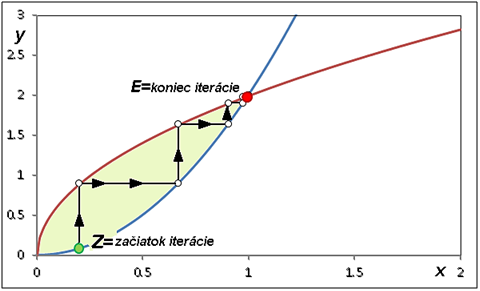
Obrázok 2 Cournotov bod E (bod rovnováhy) na reakčných krivkách
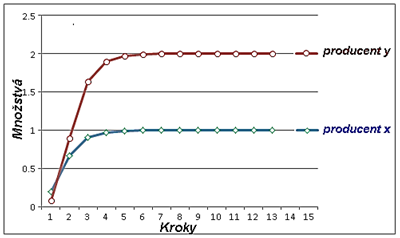
Obrázok 3 Vývoj množstiev ponuky na trhu
Situácia na takomto trhu sa dá pomocou ručnej kresby vyjadriť aj tak, ako je to znázornené na obr. 4. Na obrázku vľavo je význam skratiek nasledovný: – HN … krivka hraničných (marginálnych) nákladov; – PN … krivka priemerných nákladov; – HT … krivka hraničných (marginálnych tržieb); PT … krivka priemerných tržieb. Ako na kresbe vidno, priesečníkom hraničnej krivky nákladov a hraničnej krivky tržieb sa vedie kolmica smerujúca do bodu v ktorom sa dotýka krivka priemerných nákladov priamky priemerných tržieb. Keď sa to prenesie do súradnicovej sústavy <x, y>, t. j. množstvo x producenta A, ako aj množstvo y producenta B, získavame bod najlepšej reakcie oboch producentov na pravom grafe obr. 4.
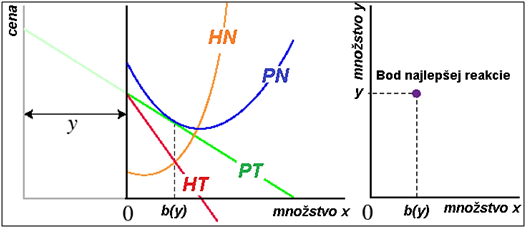
Obrázok 4 Ručná kresba situácie na duopolnom trhu
Predpoklad, že obaja producenti dokážu ihneď po zistení situácie, ktorá vznikla na základe ich predchádzajúcich rozhodnutí (v mínus jeden krok) musíme uznať, že je pritiahnutý za vlasy. Producentom totiž trvá určitý čas, než sa im podarí prispôsobiť množstvo dodávky na trh k zmenenej situácii.
Inými slovami adaptácia na zmenenú situáciu vyvoláva komplikácie v evolučnom procese. Ak by sme museli zotrvávať na použití matematických nástrojov, ktoré boli k dispozícii v čase, keď Cournot tvoril svoju teóriu, stáli by sme pred viacerými veľmi náročnými matematickými úlohami, ak by sme chceli názorne zviditeľniť onen komplikovaný evolučný proces.
Našťastie, rozvoj IKT a osobitne teórie a aplikačných možností komputačnej inteligencie nám mimoriadne dobre pomáha v reprezentácii niekedy až ťažko pochopiteľných komplexných procesov, a to napriek tomu, že matematický model duopolu zostáva stále pomerne jednoduchý. Najprv sme použili na vytvorenie vizuálnej reprezentácie softvérové prostredie iDMC.
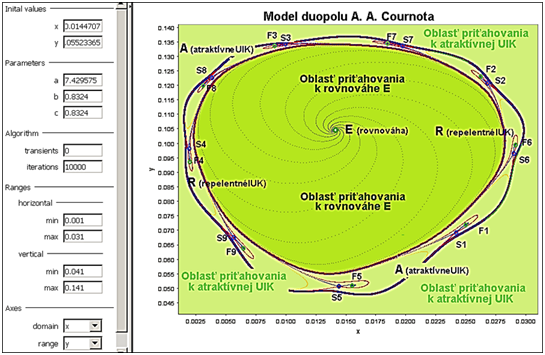
Obrázok 5 Komplikácie vyvolané jednotným adaptačným parametrom 0.8324 a pomerom 7.42975
Aby sme už na začiatku nekomplikovali výklad, budeme sa v ňom usilovať iba o komentovanie získanej situácie na obr. 5 a až neskoršie objasníme, ako sme túto snímku vytvorili v iDMC. Oproti pôvodnému modelu s okamžitými reakciami, t. j., keď by vlastne adaptačný koeficient b = c ak by tam bol vložený, tak by mal hodnotu jeden, nastala zmena spočívajúca v hodnote b = c = 0.8324 a pomer hodnôt hraničných nákladov bol 1:7.42975, takže a = 7.42975. Východiskové množstvá produktov sme nastavili na simuláciu tak, aby počítač kreslil graf vhodne na sledovanie do priestoru prvého kvadrantu so všetkými vlastnosťami modelu, ktoré by sa tam mohli objaviť, t. j. x0 = 0.144707 a y0 = 0.05523365.
Musíme však vysvetliť, že ak chceme získať podrobnejšie pohľady na niektoré oblasti musíme uskutočniť nové simulácie s vhodnými začiatočnými nastaveniami x0 a y0. Tak sme totiž dostali jednotlivé snímky potrebné k obr. 5 a premietli sme ich priehľadne na seba.
Výsledkom našich simulácií v prostredí sú nasledovné útvary: – Cournotov bod E (rovnováha) a jeho oblasť priťahovania (odborne bazén atrakcie); – bazén atrakcie bodu E ohraničuje UIK t. j. uzavretá invariantná krivka s vlastnosťou odpudzovania (repelentná UIK); – oblasť, t. j. bazén za touto krivkou je plochou, z ktorej sú začiatočné body simulácie priťahované buď k atraktívnej UIK, alebo alternatívne k deviatim dvojiciam bodov s vlastnosťou sedlo, resp. fókus (ohnisko) čoho trajektóriou je špirála; – oblasť za atraktívnou UIK je mimoriadne komplexná a nateraz nemá relevantný význam sa ňou zaoberať.
Z tohto komentára si čitateľ už môže utvoriť akú takú predstavu o tom, že aj celkom jednoduché matematické modely môžu viesť k veľmi komplikovaným situáciám, čo iba na základe matematickej analýzy bežný čitateľ nemá možnosť postrehnúť. Musel by mať solídne matematické predpoklady a vyvinuté zručnosti. Pravda dnes máme ešte lepšiu možnosť vytvárania predstáv o tvorbe zložitostí na jednoduchom izolovanom trhu. Tou možnosťou je priame simulačné experimentovanie s vhodným modelom duopolu v prostredí iDMC. Tomu sa budeme venovať na budúci týždeň.




