Maximalizácia zisku a princíp pretrvania

Ako sme ukázali v predchádzajúcich častiach výkladu, v ekonómi prevláda viera, že podnikatelia musia maximalizovať zisk, princíp ktorý si aj reálni podnikatelia osvojili a v praxi ho aj používajú. V skutočnosti nad týmto princíp stojí ešte vyšší princíp a to princíp čo najdlhšieho pretrvania. Je pozoruhodnou skutočnosťou, že maximalizácia zisku môže byť a často aj je v protirečení s tým princípom, takže maximalizácia zisku býva aj kontraproduktívna. Maximalizácia dĺžky pretrvania jedinca, druhu, celej populácie a dokonca života ako špecifickej entity na planéte Zem je prírodným princípom, ktorý nevymysleli ľudia. Na druhej strane princíp maximalizácie zisku je ľudský vynález, má teda subjektívny pôvod. V tejto časti výkladu rozvinieme dôsledky požiadavky maximalizácie zisku aj na prípad monopolu, tak ako sme to už ukázali na predchádzajúcich prípadoch, osobitne na prípade duopolu.

V predchádzajúcom výklade sme neidentifikovali spôsob získania parametra označeného symbolom k. Ako vyplýva z panujúcej ekonómie podnikateľ, teda aj monopolista je zainteresovaný na maximalizácii zisku. Rovnice, ktoré sú na to v mechanistickom prístupe potrebné, t. j. tržba a náklady, presnejšie ich marginálne podoby, MT a MN sme už skôr uviedli vo štvrtej časti. Formulácia tejto úlohy má podobu MT – MN = MZ, po doplnení vzorcov to bude MZ = (A – E) – 2(B – F)x + 3(C – G)x² – 4Dx³. Na získanie neznámej funkcie zisku musíme ešte MZ vynásobiť množstvo x, takže dostávame hľadaný vzťah

Z = (A – E)x – (B – F)x² + (C – G)x³ – 4Dx⁴ .

Táto úloha by nemusela byť príliš náročná, keby monopolista poznal funkcie z ktorých to bolo odvodené a teda, že sú tam určité hodnoty parametrov súčty a rozdiely, súčiny a najmä, že sú tam exponenty na druhú, na tretiu a na štvrtú. Lenže on okrem dvoch-troch bodov dopytu ktoré pozná, celú krivky dopytu nepozná. Predpokladajme (my to vieme! monopolista nevie), že monopolista zistil veľkosť minulého zisku pri danej veľkosti množstva dodaného na trh a má možnosť voliť dĺžku kroku a nasledujúce množstvo dodávky, takže nasledujúci bod zistíme takto

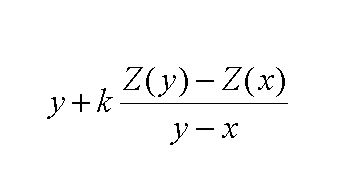, kde neplechu robí v deliteli rozdiel, ktorý by mohol byť nulový a hrozilo by tak delenie nulou. Tomu sa treba vyhnúť takto

.

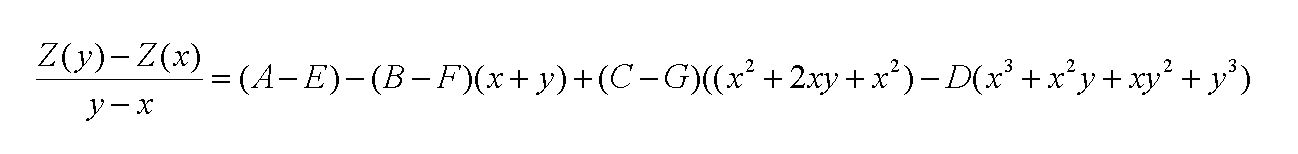
Aby sme sa mohli vrátiť do situácie ktorú sme experimentovali v predchádzajúcom výklade, použijeme tie isté hodnoty parametrov ako predtým a tak rovnicu pre hľadanie môžeme prepísať takto

.

Vyšli sme pri vytvorení tejto funkcie z toho, že pri dvojrozmernom hľadaní spočívajúcom na posune o jeden krok je projekcia definovaná nasledovne

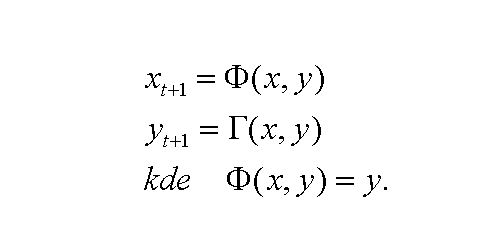
Využitím rutiny iDMC s názvom sme získali snímku reakcií množstva x na rastúcu hodnotu parametra k, obr. 1.  Na snímke zisťujeme postupné zmeny riešení na rastúcu hodnotu parametra k. Pri hodnotách menších ak k = 5/3 sú riešenia stabilné a rovnováha je fixná, po prekročené tejto hranice riešenia bifurkujú do dvoch štvorhranových orbít, ktoré rotujú doprava, ako sme ukázali v predchádzajúcom výklade a pri ešte väčších hodnotách rastú komplexity až sa dosiahnu prahy po ktorých nastupuje deterministický chaos. Aby sme to

 

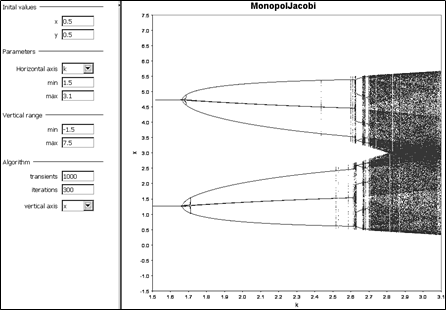
Obrázok 1 Bifurkačný portrét k oproti x

demonštrovali urobíme podrobnejšiu analýzu zhruba v intervale 2.4 < k < 2.75, výsledok je na obr. 2. Zo snímky je jasné, že pri vyšších hodnotách proces bifurkuje intenzívnejšie a napokon preskočí do typického deterministického chaosu pre obe polohy na snímke.

 

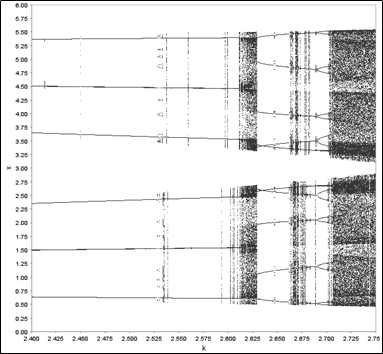
Obrázok 2 Zväčšenina v intervale 2.4 < k < 2.75

Z podrobnejšieho bifurkačného portrétu sme vybrali na pokus hodnotu k = 2.66 a urobili sme experiment v rutine iDMC s názvom Trajectory obr. 3. Dva päťuholníky sme dosiahli až po tri tisíc krokovom posune začiatku experimentu.

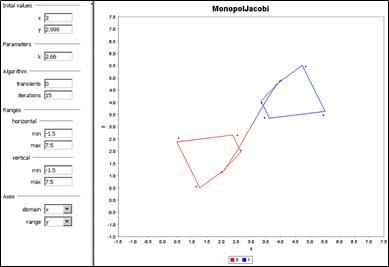
Obrázok 3 Experiment s dvomi päťhranovými orbitami – päťuholník nerotuje

 

Na rozlíšenie sme znázornili len body vrcholov a čiary ukazujú iba niekoľko krokov od nulového kroku začiatku experimentu. Stavový bod poskakuje nad fixnými vrcholmi päťuholníka. Na obr. 4 sme vystavili snímku z experimentu uskutočneného v rutine iDMC Trajectory, ale v časovo-krokovom režime pre premennú x. Dá sa jasne rozoznať, že poskakovanie v 5 – cyklovom režime sa ustavične opakuje, čo sme sa snažili zvýrazniť číslicami. Spojovacie čiary sú iba pomyselné a majú význam len ilustračný, stavový bod počas experimentu poskakuje a až po mnohých krokoch ( tu po 3000) dosiahne ustálený stav 5 – cyklového režimu. To isté v kvalitatívnom zmysle by sme dosiahli, keby sme experimentovali v pravom hornom kvadrante. Na obr. 5 sme vystavili snímku výsledkov z experimentu s hodnotou k = 2.7. Vidíme, že pri tomto drobnom predĺžení kroku sa cyklus s

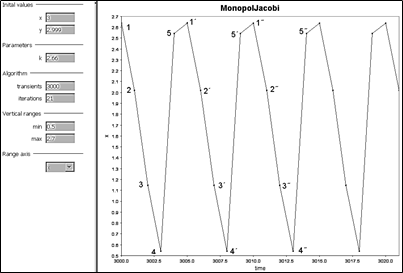
Obrázok 4 Stavový bod poskakuje v čase po vrcholoch jedného z dvoch päťuholníkov

piatimi vrcholmi znásobil dvoma na 10 – vrcholový cyklus. Ponechávame na čitateľa, aby si urobil vlastné závery o vplyve uplatňovania stratégie maximalizácie zisku na povahu procesu a na zvyšovanie komplexity, hoci sa stále pohybujeme v mechanickom prostredí. Je tu však určitá výzva a pomoc na utváranie predstáv aj pre reálneho podnikateľa s využitím komputačných experimentov hoci len v jednoduchom softvéri iDMC.

 

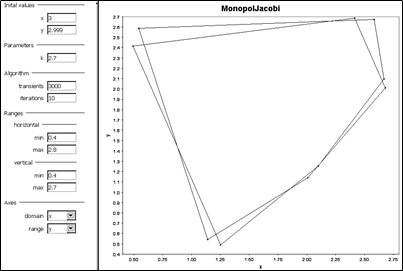
Obrázok 5 Poskakovanie v čase po nehybnom desaťuholníku

Kto sa chce stať monopolistom s produktom horizontálnej diverzifikácie môže týmto, hoci len mechanickým spôsobom zistiť aké ťažkosti ho čakajú a neminú. Nebude to mať vôbec jednoduché hoci ľahkoverní čitatelia učebníc ekonómie sú presvedčení o opaku. Lebo aj pre monopolistov platí pravda vystihnutá povzdychom veriaceho z Hrubého kostola v Trnave: „Život je tašký – jeden z najtašších!“, tak ako pre každého iného smrteľníka.

Pokračovanie nabudúce!