Trh s jedným výrobcom: monopol (diel štvrtý)
Varovanie veriacim v predsudky a mechanické modely hospodárstva: Do stredu dráhy životnej som vkročil, keď obklopil ma temný priestor lesný pretože prv som z pravej cesty zbočil. Dante Alighieri, Peklo, Spev prvý.
V už viackrát spomínanej učebnici Samuelsona a Nordhausa sa môžeme dočítať, že monopolista si sám určuje cenu a množstvo tovaru, ktoré chce dodávať na trh. Píše sa tam: “Aby firma maximalizovala svoj zisk, musí nájsť rovnovážnu cenu a rovnovážne množstvo…“. (slovenské vydanie z roku 1992, s. 157). To sme už v predchádzajúcom výklade z rôznych strán a prístupov ukázali v komputačných experimentoch. Na iných miestach učebnice sa dôvodí, že monopolista musí urobiť to, čo v prípade dokonalej konkurencie urobí trh. Sú v onej učebnici a v jej preklade do slovenčiny aj iné zjednodušenia ale ajniektoré ďalšie chyby a prehrešky proti korektnému uvažovaniu o hospodárstve v objektívnej realite a jeho zodpovednému vysvetľovaniu. Avšak pri takýchto konštatovaniach by sme mohli „začať už od Adama“, totiž od klasika politickej ekonómie A. Smitha a v ekonómii sa to hojne vyskytuje dodnes.
Teória alebo ešte presnejšie model monopolu je ďalší prípad situácie vytrhnutého z celostného komplexu – zo sociálno-ekonomického organizmu. Je pozoruhodné, že sám Samuelson kedysi dávno upozorňoval na možné nedorozumenia pri konštrukcii záverov o celostnom hospodárstve na základe vytrhnutých z kontextu jednotlivostí. Použil na to príklad staroindickej bájky o skupine nevidomých tulákov, ktorí keď stretli slona jeho ohmatávaním sa snažili zistiť čo to je. Je pochopiteľné, že sa im to nemohlo len tak ľahko podariť lebo každý identifikoval iný

Obrázok l Kresba nevidomých tulákov a slona
objekt na základe svojej vlastnej obrazotvornosti a tej časti slona, ktorú ohmatal. Z toho vidno, že mal jasno o nedostatočnosti skúmania jednotlivostí a o tom, že pomocou nich sotva možno vytvoriť kvalitnú predstavu o celku, napriek tomu zostával verný skúmaniu jednotlivostí a závery o celku odvodzoval z nich, ak vôbec. V učebnici ku ktorej sa vyjadrujeme sa na s. 568 (kap. 24 českého vydania) píše o monopole takto: „ … případ jediného prodávajícího s úplnou kontrolou odvětví. Je ve svém odvětví jediným vyrábějícím a neexistuje odvětví vyrábějící substitut blízký jeho statku.“. Takýmto prípadom môže byť výrobca, ktorý prichádza na trh s úplne novou úžitkovou hodnotou, ktorej výrobný postup zatiaľ nijaký konkurent nedokáže napodobniť a dodávať tak na trh rovnocenný statok, ide teda o horizontálnu diverzifikáciu tak produktu, ako aj výrobnej technológie. Pochopiteľne takáto situácia môže na trhu byť iba dočasná a to či bude krátka alebo dlhšia závisí od viacerých okolností najmä od pokroku v základnom a aplikovanom výskume, v technickom a technologickom pokroku ako aj v manažérskej erudícii a konkrétnom podnikateľskom výkone monopolistu. V súvislosti so skúmaním a vysvetľovaním monopolu považujeme za dôležité pripomenúť, že u viacerých ekonómov prevláda málo, ba ničím nepodložená predstava, že si monopolista môže slobodne určovať ceny a v pomere k nim aj množstvá tovaru, ktoré dodáva na trh a ten tie ceny a množstvá prijme.
Čítajte tiež:
Prvý diel: Samuelsonova učebnica Economics – liturgia ekonómov
Druhý diel: Komplikácie na strane ponuky izolovaného trhu
Tretí diel: Experimentovanie čitateľov
Spolu s tým sa často stretávame aj s predstavou, že v dôsledku týchto predností si monopolista vie optimalizovať svoj zisk. Také niečo sa často tvrdí aj v učebniciach a nami uvádzaná kniha nie je výnimkou, hoci sa tam netvrdia také jednostrannosti príliš okato. Považujeme za prirodzené, že trh na monopolistove rozhodnutia však reaguje sebe vlastným spôsobom. Na rozdiel od takýchto nepresných predstáv, ba predsudkov v realite existuje viacero prekážok, ktoré také konanie monopolistovi znemožňujú alebo aspoň komplikujú. Ťažkosti monopolistu, ktorý prichádza na trh s horizontálne diverzifikovaným tovarom sa pokúsime priblížiť na nasledovnom experimentovaním na simulačnom modeli, ktorého matematický základ sme si vypožičali od nordického ekonóma s menom Tönu Puu (kniha: Nonlinear economic Dynamics, Springer, 1997, ss. 115 – 126). Na tieto účely sme použili tak ako v predchádzajúcich príspevkoch simulačný prostriedok s ktorým sa ľahko narába a jeho ďalšou prednosťou je, že je voľne dostupný na internete teda už známy softvér iDMC. Hoci tento softvér nie je úplne dokonalý po systémovej a programátorskej stránke, je užitočným a efektívnym (ba aj veľmi efektným) pomocníkom pri experimentovaní s ekonomickými modelmi, ktoré si záujemcovia v ňom ľahko dokážu vytvoriť, takže to tu aj my využijeme.
Podľa vyššie uvedených tvrdení monopolista nepozná dosť dobre dopyt po svojom tovare. Mohli by sme však pripustiť, že pozná aspoň niekoľko jej bodov. To pravdaže nestačí na to, aby mohol plánovať objem výroby a určiť cenu, resp. predovšetkým vyriešiť celkovú optimalizačnú úlohu zisku. Aj v prípade marginálnej tržby môže nanajvýš len interpolovať tvar z niekoľkých už predtým známych bodov. Lenže takéto informácie majú len lokálny a krátkodobý význam a hlavným problémom je, že monopolista z takých informácií nevie zostaviť plán a ani netuší, že v globále existujú rôzne, napríklad dve od seba sa líšiace maximá zisku. Východiskom z tejto nepríjemnej situácie môže byť návrh zastreľovacieho spôsobu riešenie ťažkostí a ešte lepšie, adaptívneho vyhľadávacieho algoritmu pre optimum zisku z neznámej funkcie zisku. K tomu, aby sme mohli naformulovať takúto funkciu zisku, ktorá je „skrytá“ pred monopolistom musíme ešte predtým naformulovať funkciu dopytu, funkciu marginálnych nákladov a funkciu marginálnych výnosov. Pritom je však veľmi dôležité uvedomiť si čo sú predpoklady analytika a čo môže vedieť alebo aj nie daný monopolista. Je zrejmé, že monopolista nemôže vedieť všetko to, čo o skôr uvedenej situácii vie analytik, resp. čo predpokladá a aké kladie podmienky na analýzu. Priblížime to pomocou nasledovného diagramu obr. 2, ktorého krivky sme vytvoriliv Excele. Na obr. 3 ukazujeme
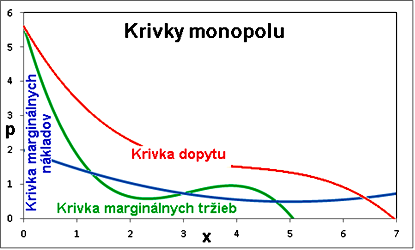
Obrázok 2 Krivky vytvorené v Excele
tzv. zastreľovanie sa analytika, na daných krivkách, ktorým sa znázorňuje možné správanie monopolistu. Keďže krivku dopytu a krivku marginálnych tržieb nepozná musí odhadnúť prvú cenu pre tovar, ktorý posiela na trh. Ako vidno na obrázku odpoveďou trhu na cenu p = 3 je vykúpenie množstva x = 1.294 jednotiek. Takto monopolista zistil prvý bod krivky dopytu. V druhom kroku zase odhadom volí cenu p = 1.412. Pri tejto cene je dopyt x = 4.706 jednotiek. Povedzme si, že monopolista sa správa racionálne, takže si zvolí strednú cenu medzi prvou a druhou voľbou, t. j. 1.412 + (3 – 1.412)/2 = 2.206 = p. Odpoveďou trhu je dopyt x = 2.2035 jednotiek. V tejto situácii, ak bude monopolista pokračovať v stratégii polenia cenového intervalu bude mať dve nové možnosti a to voliť polenie nad alebo pod treťou voľbou a tak pokračovať až kým nezistí optimálnu cenu a k nej optimálnu dodávku na trh. Vidíme, že je to pre monopolistu dosť náročný proces a jeho výrobné možnosti nemusia byť natoľko pružné, aby mohol uskutočňovať také veľké skoky aké sme ukázali, takže proces môže byť ešte dlhší a náročnejší, než sme sa sprvoti predpokladalo. Nemali by sme však pritom zabúdať, že stále ide iba o mechanický, hoci aj oveľa sofistikovanejší model vytrhnutý z kontextu celkového trhu. Preto treba so závermi z jeho analýzy prichádzať veľmi opatrne. Na druhej strane však pri dostatočnej obozretnosti už aj takýto model umožňuje lepšiu predstavu o ekonomickej komplexite. Skôr spomínaná matematický ekonóm T. Puu vymyslel oveľa elegantnejší spôsob ilustrácie daného komplikovaného procesu.
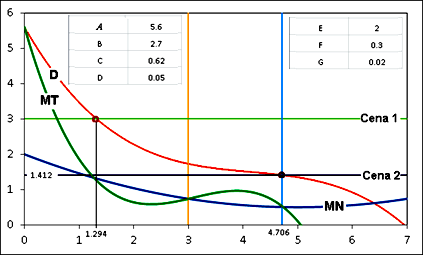
Obrázok 3 Znázornenie zastreľovania sa
Aby sme už na tomto stupni výkladu príliš nezaťažili čitateľa matematikou, pristúpime priamo k ukazovaniu výsledkov experimentov, ktoré sme dosiahli v našom virtuálnom laboratóriu vytvorenom v iDMC použijúc vzorce, ktoré sme si požičali od T. Puuho. Tu je naša konštrukcia v iDMC:
„–@@name = “MonopolJacobi”
description = “See Model refs in user’s guide”
type = “D”
parameters = {“k”}
variables = {“x”, “y”}
function f(k, x, y)
x1 = y
y1 = y + k*(3.6-2.4*(x+y)+0.6*((x^2)+x*y+y^2)-0.05*((x^3)+(x^2)*y+x*(y^2)+y^3))
return x1, y1
end
function Jf(k, x, y)
return
0, 1,
-2.4*k+1.2*k*x+k-0.15*k*(x^2)+2*k*x+k, 1-2.4*k+k+2*k*y+k+2*k*y+3*k*y^2
end“
Je dôležité si uvedomiť, že monopolista môže zastreľovaním získať len niekoľko izolovaných bodov dopytu a nie krivku. Keďže monopolista nepozná krivku dopytu, nemôže poznať ani marginálnu krivku tržieb, pretože tá predstavuje jej deriváciu. Takže tu sa dostávame do bodu výkladu, keď sa už nedá matematika vynechať. Najprv uvedieme vzťah krivky dopytu, ktorá je kubická, t. j. p = A – Bx + Cx2 – Dx3, kde p označuje cenu a x množstvo tovaru parametre A až D sú konštanty a ich hodnoty sú uvedené na obr.3 vľavo hore. Keďže tržba je podľa učebníc ekonómie súčinom ceny a množstva platí vzťah T = p ´ x. Ak vypočítame naznačené násobenie dostaneme vzťah pre celkovú tržbu, teda pre jej krivku T =Ax – Bx2 + Cx3 – Dx4. Lenže my potrebuje krivku marginálnej tržby MT, ktorú dostane prvou deriváciou vzťahu T, t. j. MT = A – 2Bx + 3Cx2 – 4Dx3, takže už máme formuly pre vytvorenie dvoch kriviek a to krivky dopytu a krivky marginálnych tržieb. Chýba nám už len tretia krivka a to marginálna krivka nákladov, tá bude MN = E – 2Fx + 3G2, ktorú sme podobne ako v prípade tržieb dostali deriváciou z formuly celkových nákladov. Aj hodnoty konštánt E, F a G nájde čitateľ na obr. 3 ale vpravo hore. Podľa učebnice štandardnou podmienkou na maximalizáciu zisku (cieľ podnikateľa maximalizovať zisk je tiež štandardná požiadavka ktorú mu nasadila do hlavy učebnica) je rovnosť MT = MN, čo na obr. 3 predstavuje prostredný priesečník týchto dvoch kriviek. Sú tam však aj dva ďalšie priesečníky a to vľavo a vpravo od prostredného, čo pravdaže vnáša do problematiky značné komplikácie. Čiastočne to pochopíme, keď budeme dôsledne pozorovať výsledok experimentu uvedený na obr. 4.
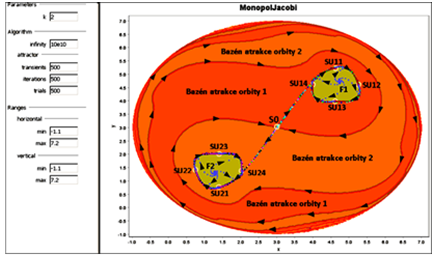
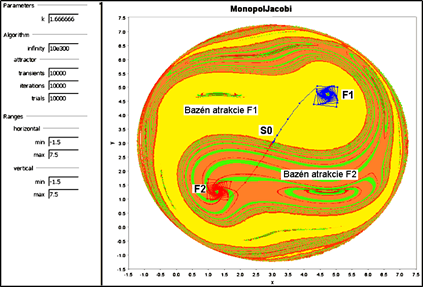
Obrázok 4 Znázornenie bazénov atrakcie stavového bodu monopolu
Oboznamujeme sa so značne komplexnou situáciou, ktorá je však pozorovateľná len nami a monopolistovi je skrytá. Na snímke vidíme tri fixné body, t. j. dva repelentné fókusy vľavo dole F2 a vpravo hore F1 a sedlový bod v strede S0, čitateľ si to určite porovná so situáciou na obr. 3. Fókusy sú vnútri zelených bazénov z ktorých je stavový bod priťahovaný na štvorhrannú orbitu, ktorá rotuje pravotočivo. Takisto je stavový bod priťahovaný z vonkajšej strany, pričom okrovú farbu sme rozlíšili na svetlú a tmavšiu. Tieto vonkajšie bazény ohraničujú štyri vetvy sedlového bodu S0. Hranicu elipsovej plochy tvorí UIK s vlastnosťou repelencie, takže ak je začiatočný stavový bod umiestnený do bielej plochy uniká do nekonečna. Aby si čitateľ mohol urobiť predstavu o časovom (krokovom) vývoji, zaradili sme snímku z časového experimentu, obr. 5, ako aj snímky na obr. 6 a 7, ktoré pri dôkladnom štúdiu odhalia mnohé skryté zložitosti pred ktorými stojí monopolista a horizontálne diverzifikovaným produktom, aj keď sa stále pohybujeme len v rovine mechanického uvažovania o izolovaných situáciách na trhu.
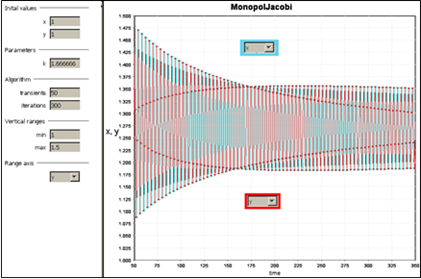
Obrázok 5 Ukážka časového vývoja od krokov 50 do 350
Obrázok 6 Bazény atrakcie F1 a F2
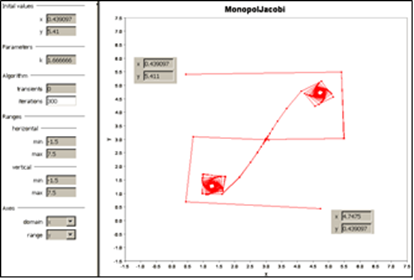
Obrázok 7 Konvergencia k sedlu a potom do jedného z dvoch atraktívnych fókusov
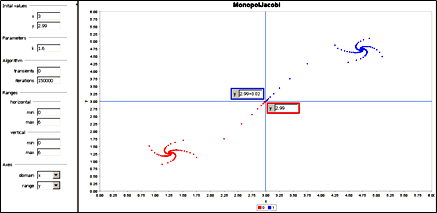
Obrázok 8 Evolúcia k jednej alebo druhej stabilnej rovnováhe
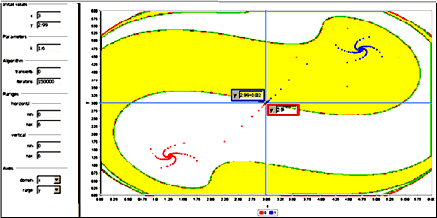
Obrázok 9 Bazény atrakcie červeného a modrého fókusu
Pokračovanie nabudúce




