Ekonomické a ekologické modely
Ekonomické teórie osnované na mechanistických predstavách a v rámci nich formulované matematické modely predstavujú určitú avšak veľmi približnú aproximáciu objektívnej hospodárskej reality. Určite nie s nadšením musíme konštatovať, že Samuelsonova učebnica nezriedka na také počínanie priamo navádza dokonca sám autor to tak robí. V dôsledku slabej korešpondencie medzi exaktnými výsledkami matematickej analýzy takých modelov a v ostatnom čase aj výsledkami ich experimentovania v komputačných laboratóriách na jednej strane a objektívnou hospodárskou realitou na strane druhej možno ľahko skĺznuť na scestie pri formulovaní záverov a identifikácii výsledkov s realitou. V horšom prípade, ak sa vyjadríme metaforicky môže taký horlivý identifikátor ocitnúť v situácii blúdiaceho v pekle, ako to opísal vo svojom slávnom spise Božská komédia Dante Alighieri. Preto naše volanie po opatrnosti by nemalo „zapadnúť prachom“. Samozrejme takéto súdy ktoré sme už aj skoršie viackrát vyslovili sa netýkajú len ekonómie ale aj ďalších vied zaoberajúcich sa štúdiom živých organizmov, ak sa tiež snažia, neraz nenáležite používať mechanistické modely na zobrazovanie živej reality. Pravda nie v každom takom prípade musia byť posudky také ostré ako v prípade ekonómie. To možno povedať napríklad o modelovaní v ekológii, ktoré je nápadne blízke formám používaným v ekonómii. V tomto pokračovaní našej analýzu a výkladu sa pozrieme bližšie na matematické formalizovanie procesov v biológii, presnejšie v odbore ekológia populácií.
Jedným z prvých vedcov, ktorí začali uvažovať o raste populácie v matematickom, aj keď vo veľmi jednoduchom zmysle bol anglikánsky historik a ekonóm T. R. Malthus. Pokúšal sa vytvoriť systematickú teóriu ľudskej populácie vo svojej knihe Esej o princípe populácie (Essay on the Principle of Population 1798), v ktorej sa opieral aj o pozbierané empirické údaje. V ďalších vydaniach svoje vývody rozvíjal a zdokonaľoval, opieral sa síce o matematické podobenstvá ale k výslovnému využitiu už vtedy existujúcej matematickej teórie diferenciálnych rovníc sa nedostal. K problematike sa snažil priblížiť metaforou o aritmetickej a geometrickej postupnosti čísel pričom tvrdil, že životné potreby sa vyvíjajú lineárne, t. j. aritmetickým radom 1, 2, 3, 4, 5, 6, 7, 8, 9, … atď. zatiaľ čo ľudská populácia má tendenciu rásť radom geometrickým 1, 2, 4, 8, 16, 32, 64, 128, 256, …atď. ak nejaké
Obrázok 1 T. R. Malthus 1766 – 1836
iné príčiny tomu nebránia. No a práve tými riešeniami na pribrzdenie rastu ľudskej spoločnosti vošiel do dejín veľmi negatívnym spôsobom: za riešenia totiž považoval vojny, prírodné katastrofy, pandémie a pod. Veľmi zjednodušene sa dá Malthusova diskrepancia medzi rastom životných potrieb a rastom ľudskej populácie vyjadriť pomocou rastúcej priamky a krivky, ak je to znázornené na obr. 2. Matematický formalizmus v pravom slova zmysle použil na danú problematiku až o 50 rokov neskôr belgický matematik-biológ Pierre-Francois Verhulst (1804 – 1849) svojou formuláciou
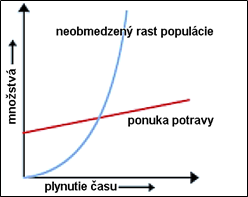
Obrázok 2 Grafy diskrepancie podľa Malthusa
logistickej rovnice, v odbornej literatúre sa cituje aj pod názvom verhulstova rovnica. Jeho prvá snaha bola zachytiť zmenu v počte živých členov populácie do korektného matematického vzorca. Viedlo to k nasledovným výsledkom v podobe diferenciálne rovnice
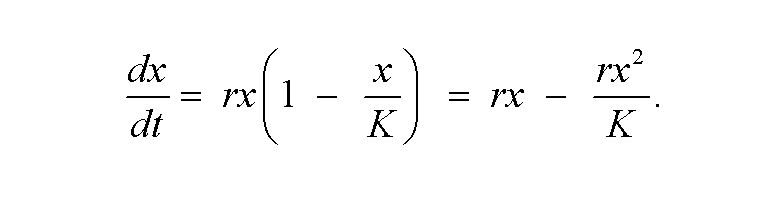
V uvedenej rovnici je K tzv. kapacitou zachovania populácie, ktorá vedie k najvyššej ešte udržateľnej hladine obyvateľstva. Premenná x predstavuje počet živých jedincov a parameter r je rastový faktor. To aký bude výsledný rast závisí od rozdielu vyjadreného na pravej strane rovnice, teda od vzájomnej veľkosti parametrov r a K. Najjednoduchšie riešenie dostaneme, ak budeme prírastok považovať za nulový t. j.
Obrázok 3 Litografický portrét P.-F. Verhulsta
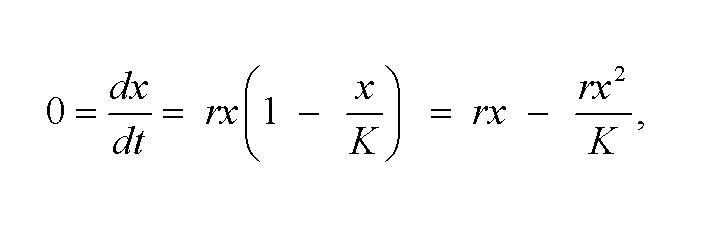
z čoho vyplýva riešenie, že
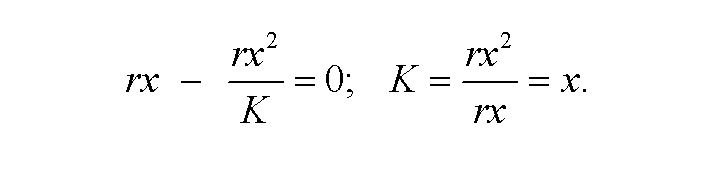
Máme teda dve rovnovážne riešenia a to 0 a K.
Samozrejme viditeľnejšie a teda aj zrozumiteľnejšie to všetko bude ak použijeme ako sme to robili už skôr komputačné experimentovanie. Logistický model v iDMC pre K = 1 a r = mu bude teraz v tejto podobe
–@@
name = “logistic map”
description = ” See Model refs in user’s guide”
type = “D”
parameters = {“mu”}
variables = {“x”}
function f(mu, x)
y = mu * x * (1 – x)
return y
end
function Jf(mu, x)
return mu – 2 * mu * x;
end
Urobíme niekoľko simulácií:
a) simulácia v rutine „Bifurcation“
Na obr. 4 jasne vidno ako sa zvyšovaním hodnoty parametra mu = r zdvojujú periódy až sa dosiahne prah deterministického chaosu a pri jeho ďalšom zvyšovaní nastáva celkom nezvyčajné chaotické správanie počas ktorého niekde deterministický chaos ustane a naskočí perióda 3, 6, 12, 24 a prechod do chaosu, obr. 5. Pri ďalšom zvyšovaní hodnoty parametra r = mu naskočí po chaose perióda 5, 10, 30 a zase chaos, pričom na obr. 6 vidíme aj ďalšie pasáže začínajúce s nepárnymi cyklami ako 7, prípadne 9 a pod. Takto sa možno veľmi názorne presvedčiť o tom, že aj najjednoduchší ekologický model, v danom prípade Verhulstova rovnica generuje veľmi neštandardné správanie s pasážami rozličných počtov cyklov a prerušovanými sú pasážami deterministického chaosu. Keďže hospodárstvo tvorí konkrétna, či menovitá populácia, teda živá spoločnosť ľudí, tieto zistenia už aj v tej najzákladnejšej biologickej rovine ukazujú vysokú komplexitu vývoja. V uvedenej súvislosti sa nám javí úplne naivné volanie niektorých ekonómov a neznalých politikov po tzv. udržateľnom raste, ba dokonca o udržateľnom rozvoji. Ak už nebudeme brať do úvahy vedecké zistenia a zostaneme len v rovine jednoduchej logiky, tak formulácia udržateľného rastu je jasný sylogizmus. Rozumný pohľad na daný politický cieľ môže byť formulovaný ako udržateľná hladina, či stav hospodárstva, teda nie tok ale stav. Je udivujúce ak nie priam groteskné ak vysoko postavený politik nevie rozoznať rozdiel medzi stavom a tokom. To je ako keď odborník na vojenstvo nazýva húfnicu kanónom či naopak.
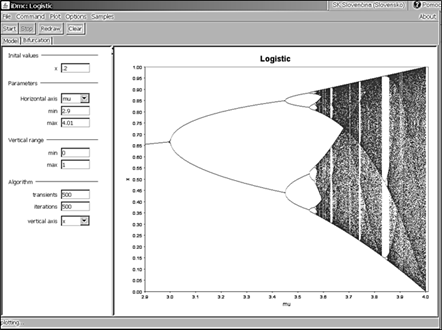
Obrázok 4 Bifurkačný portrét logistickej rovnice
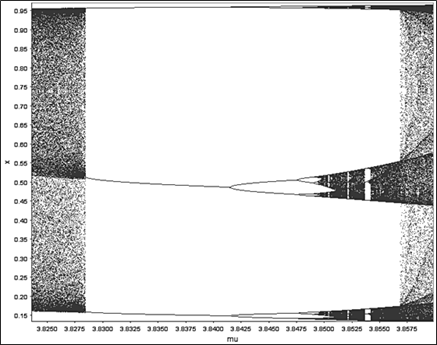
Obrázok 5 Koniec chaosu – naskočil nepárny cyklus
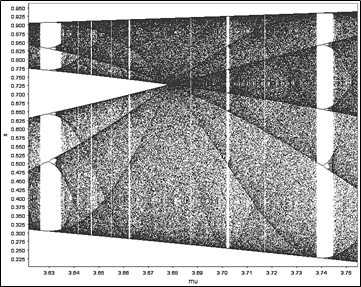
Obrázok 6 Ďalšie pasáže s nepárnymi cyklami
b) simulácia v rutine „Trajectory“/„Cobweb animation“
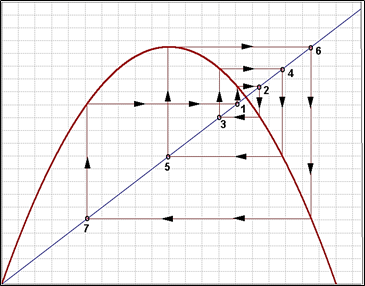
Obrázok 7 Pri hodnote r = 3.70208 naskočil 7-periódový cyklus
c) simulácia v rutine „Trajectory“/„Time“
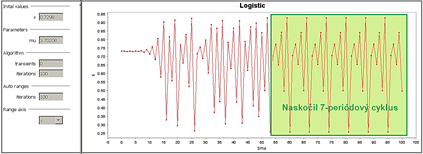
Obrázok 8 Krokovo časová evolúcia k 7-periódovému cyklu
Ale aby sme nezabudli na Verhulsta, na obr. 9 prinášame obraz logistickej krivky s tromi reálnymi údajmi o obyvateľstve Belgicka v prvej polovici 19. Storočia.
Dve populácie – spolužitie
Na predstavenie príbehu o evolúcii spolužitia dvoch populácií sme pripravili nasledujúci matematický model, ktorý sme vložili do prostredia iDMC aby sme mohli s ním experimentovať. Pretože v oboch rovniciach je rovnaký regulačný koeficient l, získané výsledky z experimentov budú symetrické, model v iDMC na obr. 12.
x1 = (1 – lamb)*x + 4*lamb*y*(1 – y)
y1 = 4*lamb*x*(1 – x) + (1 – lamb)*y
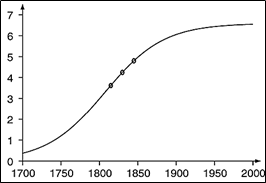
Obrázok 9 Tri reálne body na logistickej krivke
(Obyvateľstvo Belgicka v rokoch 1815, 1830 a 1845)
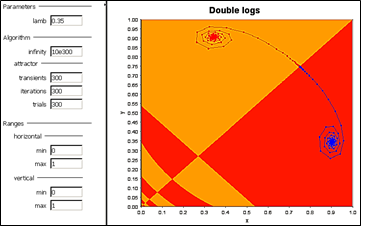
Obrázok 10 Namotávanie na jeden alebo druhý atraktívny fókus
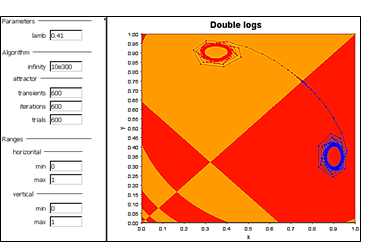
Obrázok 11 Namotávanie na jednu alebo druhú atraktívnu UIK
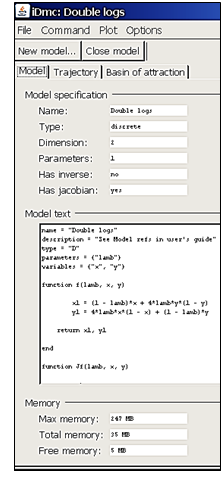
Obrázok 12 Faximile stránky z iDMC
Snímka na obr. 10 predstavuje bazény atrakcie dvoch atraktívnych fókusov. Uhlopriečka rozdeľuje celý priestor na dve polovice v ktorých sa striedajú bazény oboch fixných bodov v podobe atraktívnych fókusov. Nasledujúca snímka, ktorá vznikla zvýšením hodnoty parametra na hodnotu l = 0.41 ukazuje bifurkáciu riešenia z fókusov na UIK. Ďalšie zvyšovanie parametra l by viedla k čoraz komplikovanejším UIK útvarom a pasážam s cyklami o viacerých fixných bodov, inak povedané, riešenia by boli stále komplikovanejšie. Musíme však upozorniť na to, že až takmer sto rokov po Verhulstovi prišli dvaja vedci nezávisle od seba na myšlienku vytvoriť 2-populačný model. Jeden z nich bol taliansky matematik Vito Volterra a druhý americký matematik – biofyzik Alfred J. Lotka. Ich modely vošli do literatúry ako model dravec – korisť (predator – prey).
Obrázok 13 A. J. Lotka vľavo a V. Volterra vpravo
Ich model možno vyjadriť nasledovne
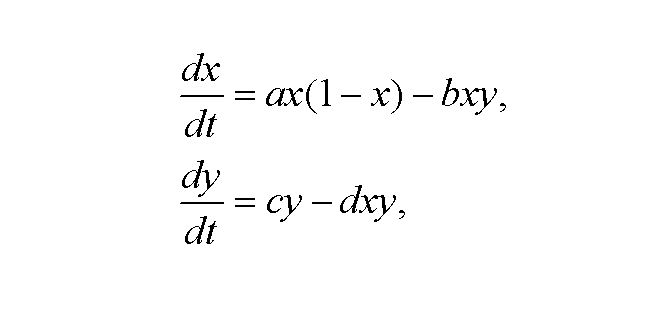kde premenné x a y sú počty členov populácií respektíve a parametre sú
a … miera rastu dravcov, b …účinnosť lovu na početnosť koristi, c … prirodzená úmrtnosť dravcov pri neprítomnosti koristi a napokon d … miera účinnosti a výsledkov pri love koristi.
Novší model zaviedli D. Fournier-Prunaret a R. Lopez-Ruíz v podobe 2D projekcie (mapy) T:
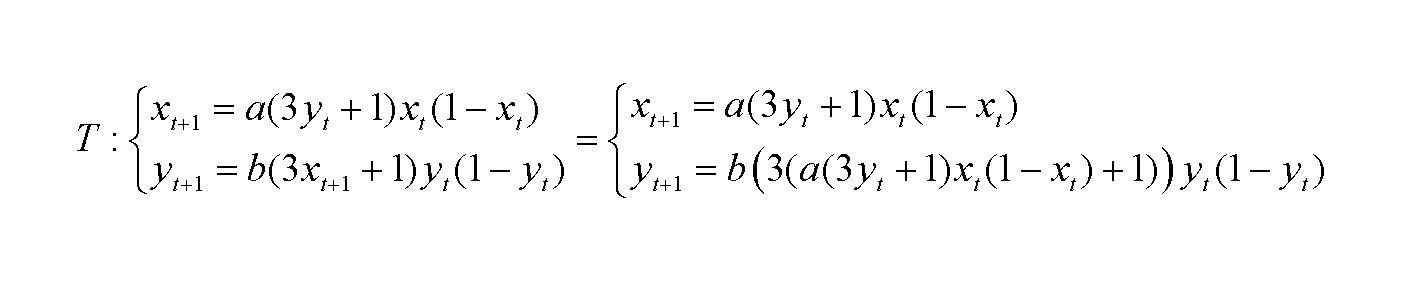
, kde a resp. b sú reálne riadiace parametre, x a y sú premenné vyjadrujúce počet jedincov v populácii, resp. biomasu populácie. Uvedené projekcia je časovo nesúmerná, lebo jedna jej čas je posunutá o jeden krok času (asymetrická spätná väzba). Komputačné experimenty ukazujú, že sústava je stabilná v rozpätí
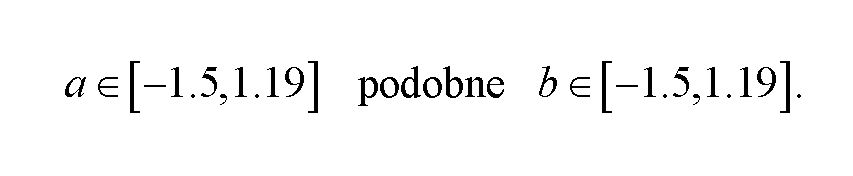
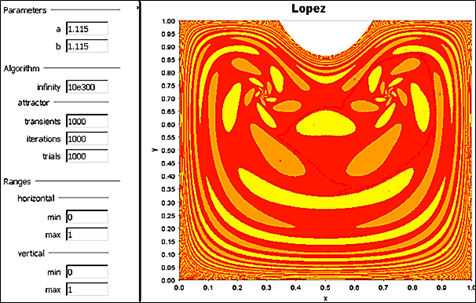
Obrázok 14 Bazén atrakcie modelu „Lopez“ v iDMC
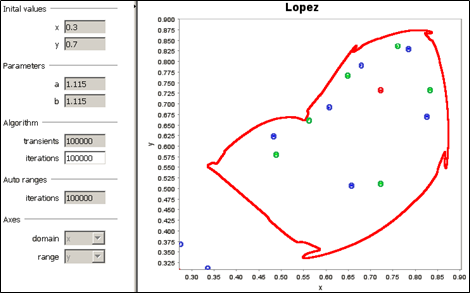
Obrázok 15 Periodické body 6 atraktívnych fókusov a 6 sediel a atraktívna UIK
Ide vlastne o dva prekrížené trojuholníky sediel a atraktívnych fókusov. V závislosti od toho do ktorého bazéna atrakcie umiestnime začiatočný bod experimentu k tej trojici periodických bodov bude evolúcia konvergovať, viď. obr. 14 a 15. Rovnovážny bod je repelentný. Hoci sú aj ekologické simulácie urobené ne veľmi jednoduchých matematických modelov ich prezeranie umožňuje hlbšie a jasnejšie pochopenie komplexít v rozvoji hospodárskych organizmoch. Isteže ide len o metafory, ale úprimne povedané modely v učebnici Samuelsona nie sú tiež iba metafory?
Podrobnejšie sa metaforami ekologicko-ekonomického vývoja budeme zaoberať v nasledovnom výklade č. 7
